Hexagonal Compacta (HCP)
Junto con la estructura cúbica centrada en las caras, la hc en una de las dos estructuras con el máximo I.C. de 12.
Si estudiamos su celda unidad podemos observar que es muy simple y da poca información sobre como están distribuidos los átomos en la estructura.
Si ampliamos la representación a varias celdas unidad se puede observar ya una estructura en capas. En una capa, los átomos se encuentran empaquetados de forma compacta; cada uno de ellos rodeado por otros seis (I.C. 6). Las capas se empaquetan de manera que los átomos de una capa se colocan en el hueco generado por tres átomos de la capa contigua. Una tercera capa de átomos se sitúa de manera que las capas alternas estén eclipsadas. Se conoce como empaquetamiento ABA.
Descripción de la estructura Hc
La estructura Hc está formada por capas compactas (con I.C. 6), que se apilan en una secuencia ABA.
Huecos tetraédricos en la estructura Hc.
En la estructura Hc, al igual que en la estructura CCCaras, se generan huecos tetraédricos. Comenzaremos diciendo que un hueco tetraédrico se genera cuando un átomo o ion se sitúa entre otros tres átomos o iones. Si dentro de la capa central seleccionamos un átomo podemos observar que, junto con tres átomos de la capa superior y otros tres de la capa inferior, forma parte de dos tetraedros. Aislando ese conjunto de átomos, podemos confirmar los dos tetraedros alrededor del átomo de referencia. En el interior de cada tetraedro se genera un hueco en el que se puede alojar un átomo o ion. No se conoce ninguna estructura en la que se ocupen todos los huecos tetraédricos de un empaquetamiento hexagonal compacto. En la siguiente figura podemos ver que ello se debe a razones estéricas. Los iones que ocupan las posiciones tetraédricas se encuentran muy próximos.
Si una red hexagonal X de aniones ocupa todos sus huecos tetraédricos por cationes M, la estequiometría del sólido será MX. Así es la estructura de ZnS.
Huecos octaédricos en la estructura Hc.
Un octaedro es un poliedro de seis vértices y ocho caras triangulares. Aunque las seis posiciones son equivalentes, frecuentemente un octaedro se representa como cuatro posiciones ecuatoriales y dos posiciones axiales situadas estas por encima y por debajo del plano ecuatorial.
Si representamos dos capas de la estructura hexagonal compacta podemos observar huecos octaédricos en los que se pueden alojar átomos o iones. Si seleccionamos alguno de los átomos/iones de la red hexagonal compacta podemos ver que se encuentra rodeado por tres octaedros de la capa inferior y otros tres de la capa superior, que no se muestran en la figura. Por ello el I.C. de ambos tipos de átomos o iones es igual a 6. Si una red hexagonal X de aniones ocupa todos sus huecos octaédricos por cationes M, la estequiometría del sólido será MX. Este tipo de estructura la adopta NiAs.
Relación c/a
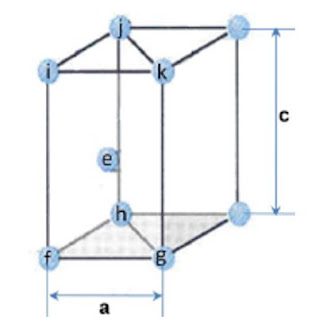
Para empezar esta demostración tenemos que definir la altura del H.C.P. siendo igual a “c”. Cada uno de los lados del hexágono que se encuentran en los planos superior e inferior será igual a “a”. Analizando la estructura se puede observar que se puede dividir en tres sub estructuras iguales, con lo que se procede a realizar el análisis de los triángulos internos.
Teniendo en consideración que al dividir la estructura los triángulos obtenidos son equiláteros (lo que nos dice que sus lados son todos iguales) y tendrán un valor de “a” sus lados. Sumado a esto, se asume el principio de “esfera rígida” donde el punto “e” se encuentra equidistante de los planos superior e inferior y también se encuentra a c/2 de dichos planos y la distancia de ef = eh = fh = fg = gh = eg = a = 2r
Si analizamos el tetraedro formado por los puntos “e”, “f”, “h” y “g” se tiene la proyección de “e” la cual se llamará “i” y lo consideraremos como el baricentro del triángulo “fhg”.
Como “i” es el baricentro, el segmento fi es la bisectriz del ángulo “fhg” que tiene un valor de 60° por ser un triángulo equilátero, entonces decimos que:
hfi = ifm
fhg= fhi + ifm
fhg = 2 ifm
60°/2 = ifm
Ifm = 30°
Como “i” es el baricentro “im” es la mediana del segundo segmento fg y “m” el punto medio entonces nos queda que fm = mg = a/2 y el ángulo imf = 90°
Aplicamos entonces:
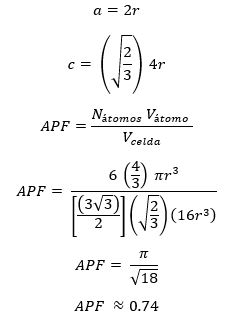
Se aplica Pitágoras al triángulo formado en “fei” y sustituimos en la ecuación para obtener:Factor de Empaquetamiento Atómico (APF) para la Hexagonal Compacta (HCP)
La longitud de un lado del hexágono será denotada por a mientras que la altura del hexágono se denotará como c. Entonces: Entonces es posible calcular el APF como sigue:
Bibliografía:







Comentarios
Publicar un comentario